practica de examen

Es de el circuito 4017 para la practica de examen

http://www.megaupload.com/?d=3HWVUS31

circuitos del proyecto

En este enlace pueden descargar los archivos de las configuraciones de los circuitos necesarios para el proyecto

http://www.megaupload.com/?d=DIODQ60V

Libro de Electronica Industrial

En la siguiente direccion pueden descargar un libro que les puede ser de mucha ayuda, no solo para la materia sino tambien para algunas otras coas que son muy interesantes, de verdad les recomiendo que lo descarguen pero sobre todo que lo revisen por que realmente es muy interesante.

http://depositfiles.com/es/files/eqbzdxgh7

Tabla de Contenidos

Capítulo 1: La Numeración Binaria

Capítulo 1: Problemas resueltos

Capítulo 2: Las Tres Funciones Lógicas Básicas

Capítulo 2: Problemas resueltos

Capítulo 3: El Algebra Boleana

Capítulo 3A: Problemas resueltos

Capítulo 3B: Problemas resueltos

Capítulo 4: El Mapa de Karnaugh

Capítulo 4: Problemas resueltos

Capítulo 5: El Flip-Flop R-S. Memorias. Multivibradores

Capítulo 5: Problemas resueltos

Capítulo 6: El Flip-Flop J-K. Contadores

Capítulo 6A: Problemas resueltos

Capítulo 6B: Problemas resueltos

Capítulo 7: Tópicos Especiales

Capítulo 7: Problemas resueltos

Capítulo 8: Lógica Multivaluada

Capítulo 8: Problemas resueltos

Suplemento # 1: Las Familias Lógicas

Suplemento # 2: El Microprocesador (µP)

Suplemento # 3: Cómo Trabaja el Microprocesador
Suplemento # 4a: Las Instrucciones del µP 8086

Suplemento # 4b: Programación del Microprocesador

Suplemento # 5: Las Comunicaciones Asíncronas
Suplemento # 6: El Amplificador Operacional

Suplemento # 7: El Temporizador 555
Suplemento # 8: El PLC. Diagramas de escalera
Suplemento # 9: Máquinas Moore. Máquinas Mealy

Bibliografía

1: La numeración binaria

1: La numeración binaria

Desde que el hombre aprendió a hacer uso de razón, se vió en la necesidad de contar de alguna manera los objetos que le rodeaban y, muy en especial, los que poseía. El florecimiento del comercio en los tiempos antiguos agravó aún más la necesidad de utilizar un sistema numérico preciso y fácil de utilizar.

De esta manera, el hombre empezó a contar de diez en diez (que es lo que hoy conocemos como el sistema decimal) influenciado por el hecho de que poseía diez dedos. Conforme ascendía la numeración, cada unidad numérica recibía un símbolo diferente (por ejemplo, 3, 4, 5 en la numeración arábiga). Después del nueve, se tomaba el símbolo que representaba la menor cantidad de unidades (el 1) y se le agregaba un cero, con lo cual se obtenía la cantidad décima. La operación empezaba de nuevo su conteo ascendente hasta llegar a diecinueve, después de lo cual se aumentaba la cifra a la izquierda en una unidad poniéndose un cero a la derecha de la misma, repitiéndose el proceso indefinidamente. Podemos observar que, sin el cero, se habría requerido un símbolo diferente para cada número mayor que nueve (por ejemplo, el símbolo A para el diez, el símbolo B para el once, el símbolo C para el doce, etc.). En efecto, sin el cero, cualquier sistema numérico resulta extremadamente complejo e impráctico (podemos imaginar los problemas que padecían los romanos cuando en su sistema de numeración romana trataban de multiplicar una cantidad por otra, cuando trataban de multplicar algo como XXIII por LIV en vez de lo que para nosotros es 23 por 54). No en vano se ha proclamado la invención del cero como uno de los más importantes avances en la historia de la humanidad.

Nuestra atención se vuelve ahora hacia un problema filosófico. Supongamos que el hombre en vez de tener cinco dedos en cada mano hubiese tenido tres. ¿Cuál habría sido nuestra forma de contar?

Un momento de reflexión nos indica que nuestro sistema numérico en tal caso no habría sido muy diferente del sistema decimal que conocemos en la actualidad. Al tener tres dedos en cada mano, nuestra inclinación natural habría sido contar de seis en seis, de la misma manera en que el hombre moderno con cinco dedos en cada mano cuenta de diez en diez. Al contar de seis en seis, la numeración ascendería de la manera siguiente:

Notamos que el sistema numérico basado en seis dedos, el sistema numérico base seis, nunca utiliza el símbolo 6, de la misma manera que en el sistema númerico base diez (o sistema decimal) no existe ningún símbolo especial para representar el número diez. Notamos también que el conteo ascendente en el sistema numérico base seis procede en forma similar al conteo ascendente en el sistema numérico base diez. Al llegar al 5, se toma el símbolo que representa la menor cantidad de unidades (el 1) y se le agrega un cero, obteniéndose así la siguiente cifra. El proceso se repite indefinidamente de modo similar al proceso utilizado en el sistema decimal. El número que sigue a 555, por ejemplo, sería 1000. Nótese que una colección de ocho objetos en el sistema decimal se representa con el número 8 mientras que en el sistema numérico base seis se representa con el número 12 (esta equivalencia se representa simbólicamente como 8₁₀ = 12₆).

Por extraño que el sistema numérico base seis nos parezca, debemos recordar que éste no nos sería tan extraño si tuviésemos tres dedos en cada mano.

Vemos pues, que la única razón por la cual contamos de diez en diez es porque tenemos diez dedos en ambas manos. Vemos también que son igualmente posibles otros sistemas numéricos, no sólo el sistema numérico base seis, sino también el sistema numérico base cuatro, el sistema numérico base siete, etc.

Podemos convertir un número cualquiera de nuestra base decimal a una base menor (por ejemplo, un número en sistema decimal a su equivalente en sistema base tres) por el método de la división sucesiva. Este método se lleva a cabo de la siguiente manera:

(1) Se divide el número decimal dado entre la base al cual queremos convertir al número, y se destaca el residuo obtenido.

(2) El cociente obtenido de la división anterior se vuelve a dividir nuevamente entre la base a la cual queremos convertir el número, y se destaca el residuo así obtenido.

(3) El procedimiento anterior se repite hasta que ya no es posible seguir dividiendo sin obtener una fracción con punto decimal. Al llegar a esta etapa, se destacan el dividendo obtenido así como el residuo.

(4) El número correspondiente a la base menor se obtiene escribiendo como el primer dígito el dividendo obtenido en el último paso anterior, y poniendo como el segundo dígito (a su derecha) el residuo obtenido del también del último paso anterior.

(5) Para el tercer dígito, escribimos a la derecha del resultado anterior el residuo obtenido de la penúltima división.

(6) El paso anterior se repite hasta que se hayan agotado todos los dígitos.

Para convertir un número en una base menor al sistema decimal (por ejemplo, un número en el sistema base siete a su equivalente en sistema decimal), se multiplica la primera cifra del número por la base menor. Al producto resultante se le agrega la segunda cifra del número y se vuelve a multiplicar por la base menor. El procedimiento se continúa hasta agotar las cifras, después de lo cual se tendrá el número decimal.

De un interés especial para nosotros es el sistema numérico base dos o sistema binario.

Si el hombre hubiera tenido tan solo un dedo en cada mano, entonces para ir contando "hacia arriba de uno en uno" en el sistema base dos o sistema binario, y tomando en cuenta que así como en el sistema decimal o sistema base diez al que estamos acostumbrados no existe un símbolo especial para representar el número diez tampoco en el sistema binario existirá un símbolo especial para representar el número dos, el conteo binario ascendente "hacia arriba" procedería de la manera siguiente:

El número binario 110 que se ha destacado con fondo de color amarillo es el que se utiliza para identificar con el símbolo "6" lo que nosotros por costumbre llamamos un sexto objeto o una colección de seis cosas. En una canasta de manzanas, el objeto, que podría ser la sexta manzana, sigue siendo el mismo independientemente de los símbolos que usemos para identificarlo. Lo único que cambia es nuestra forma de representarlo, que como hemos visto es hasta cierto punto arbitraria. (En esta lista de números binarios se ha destacado también, con fondo color ciano, el número binario que representa a un onceavo objeto.) Y así, en el sistema binario, tal vez al ir al mercado a comprar unas naranjas le diríamos a la encargada del puesto algo como "por favor deme 101 naranjas". Y si esto nos parece raro, hay que meditar que para los individuos de una civilización alienígena que tuviesen siete dedos en cada mano, dando un total de 14 dedos (con lo cual su sistema de numeración seguramente sería base 14), nuestro sistema de contar decimal tal vez les parecería sumamente extraño. Todo es cuestión de perspectiva.

¿Y por qué es de tanto interés para nosotros el adentrarnos en un sistema numérico como el sistema binario, como si no tuviéramos ya suficientes problemas con el sistema decimal?

Al tratar de utilizar circuitos eléctricos para llevar a cabo operaciones matemáticas (o bien, operaciones de control), nos encontramos con el hecho de que existen únicamente dos estados posibles que se pueden utilizar para llevar a cabo procesamiento de información. Uno es el estado de encendido, lo cual podemos representar con el número uno ("1"). El otro es el estado apagado, el cual representamos como cero ("0").

Imaginemos una hilera de cinco focos, en la cual el primer foco (a la izquierda) está apagado, los dos focos siguientes encendidos, el cuarto foco apagado y el quinto foco encendido. Representando los focos encendidos con un "1" cada uno y los focos apagados con un "0" cada uno, obtenemos la siguiente representación:

01101

Este número representa el número 13 en el sistema decimal. Cada dígito del número binario, encendido o apagado, se conoce como bit. Una serie de varios bits en sucesión como la arriba mostrada se conoce comunmente como palabra binaria o simplemente palabra. Así pues, siguiendo la costumbre legada de los árabes sarracenos, en la numeración binaria, al igual que en la numeración decimal en la cual conforme se va contando hacia arriba las cifras de magnitud creciente correspondientes a las unidades, las decenas, las centenas, etc. se van escribiendo hacia la izquierda, también en la numeración base 2 se acostumbra escribir los números binarios creciendo hacia la izquierda, y al hacer esto el "bit" de menor magnitud que es puesto en el extremo derecho es conocido como el bit menos significativo (en inglés: Least Significant Bit ó LSB), mientras que el "bit" de mayor magnitud es puesto en el extremo izquierdo y es conocido como el bit más significativo (en inglés: Most Significant Bit ó MSB).

A continuación se muestra una tabla conocida como tabla de equivalencias:

Usando tablas como ésta es posible acortar la conversión de un número en sistema binario a sistema decimal y viceversa. Por ejemplo, si se desea encontrar el equivalente decimal de la palabra 10110, notamos que:

10110 = 10000 + 100 + 10

= 16 + 4 + 2

= 22

Veamos esto mismo desde otro punto de vista, desde el punto de vista de la representación de un número usando potencias de dos. La tabla anterior de equivalencias puede ser representada usando potencias del número dos (en donde por definición una exponenciación a la potencia cero es tomada como la unidad):

2⁰ = 1

2¹ = 2

2² = 2x2 = 4

2³ = 2x2x2 = 8

2⁴ = 2x2x2x2 = 16

2⁵ = 2x2x2x2x2 = 32, etc.

Teniendo esto en mente, podemos construír una tabla de potencias de dos como la siguiente:

Esta tabla, basada en las potencias del número dos (en donde por definición la exponenciación a la potencia cero es tomada como igual a la unidad) se utiliza de la siguiente manera: Supóngase que queremos convertir el número decimal 59 a su equivalente en sistema binario. Este número es mayor que 32 pero es menor que 64, de modo tal que la primera cantidad que formará parte del mismo será 2.5=32. Si le sumamos el siguiente número inferior de la tabla, 2.4=16, la cantidad cumulativa será 48, la cual no excederá el número decimal 59, de modo tal que podemos agregar 2.4 al sumando cumulativo. Y si le sumamos el siguiente número inferior de la tabla, 2.3=8, la cantidad cumulativa será 56, la cual tampoco excederá el número decimal 59, de modo tal que podemos agregar 2.3 al sumando cumulativo. Sin embargo, no podemos agregar 2.2=4 porque la suma cumulativa excedería el número decimal 59, de modo tal que descartamos 2.2 como posible componente de la suma cumulativa. Procediendo de esta manera hasta agotar la tabla, vemos que el número decimal 59 se puede representar en potencias de dos de la manera siguiente:

59 = 32 + 16 + 8 + 0 + 1 + 1

59 = 2⁵ + 2⁴ + 2³ + 0 + 2¹ + 2⁰

Con esto, la representación del número 59 en ambas bases (la base decimal y la base 2) procede de manera inmediata consultando la tabla:

59₁₀ = (100000)₂ + (10000)₂ + (1000₎₂ + (0)₂ + (10)₂ + (1)₂

59₁₀ = 111011₂

Este resultado puede ser corroborado con el método de la división sucesiva.

Para el procedimiento inverso, esto es, convertir un número de cierta base a su equivalente en sistema decimal, podemos hacer tal cosa de manera sencilla llevando a cabo la expansión del número a través de la representación en las potencias del número en su base orignal. Por ejemplo, si queremos convertir el número binario 101001 a su equivalente en sistema decimal, la expansión sobre las potencias de dos se llevará a cabo de la siguiente manera:

101001₂ = (1)2⁵ + (0)2⁴ + (1)2³ + (0)2² + (0)2¹ + (1)2⁰

101001₂ = 32 +0 + 8 + 0 + 0 + 1

101001₂ = 41₁₀

Ahora bien; podemos sumar, restar, multiplicar y dividir en el sistema binario de la misma manera en la cual llevamos a cabo dichas operaciones en el sistema decimal.

Existe una forma especial de representar los números decimales usando el sistema binario, para que estos se parezcan un poco más a la numeración que usamos (aunque no es notación binaria pura). Cada dígito decimal se representa por su equivalente por separado, sin llevar a cabo conversión alguna. Por ejemplo, el número 3497 se representa como sigue:

Esta forma de representación se conoce como el código decimal codificado binario BCD (del inglés Binary Coded Decimal).

Ahora nos plantearemos otra dilema filosófico un poco diferente al problema con el cual comenzamos este capítulo: Supóngase que el hombre en vez de tener cinco dedos en cada mano hubiese tenido ocho. ¿Cuál habría sido nuestra forma de contar? (El caso no es tan hipotético como pudiera creerse; hay personas que de nacimiento son portadoras de una falla genética que produce en ellas algo conocido como polidactilismo, lo cual es una expresión médica para designar la presencia de más de cinco dedos ya sea en las manos o en los pies; y aunque pudiera parecer que existe alguna ventaja en poseer una mayor cantidad de dedos en ambas manos o pies que los cinco que actualmente tenemos, la evolución por alguna razón no ha favorecido una cantidad mayor de dedos).

Nuevamente, un momento de reflexión nos indica que nuestro sistema numérico en tal caso no habría sido muy diferente del sistema decimal que conocemos en la actualidad, excepto que estaríamos contando de dieciseis en dieciseis. Al tener una abundancia de dedos en ambas manos, muy posiblemente habríamos inventado algún símbolo único como el símbolo A para representar en dicho sistema numérico base-16 lo que hoy denotamos como diez con dos símbolos (10). Para representar el equivalente del número decimal 11 nuestro doceavo dedo se podría haber representado con otro símbolo nuevo, como el símbolo B. De este modo, habríamos tenido un símbolo diferente para representar cada número hasta antes de llegar al número 16 (decimal). Y al llegar a lo que vendría siendo el equivalente del número 16 decimal, se tomaría el símbolo que representa la menor cantidad de unidades (el 1) y se le agregaría un cero, obteniéndose así la siguiente cifra. El proceso se repite indefinidamente de modo similar al proceso utilizado en el sistema decimal. Un conteo ascendente en este sistema numérico hexadecimal procede de la siguiente manera:

Base 10_____Base 16

0__________0
1__________1
2__________2
3__________3
4__________4
5__________5
6__________6
7__________7
8__________8
9__________9
10__________A
11__________B
12__________C
13__________D
14__________E
15__________F
16__________10
17__________11
18__________12
19__________13
20__________14
21__________15
22__________16
23__________17
24__________18
25__________19
26__________1A
27__________1B
28__________1C
29__________1D
30__________1E
31__________1F
32__________20

Para destacar un número como un número que está basado en el sistema hexadecimal, utilizamos una letra h ya sea al final del número o al principio del número o como subscripto del número. Así, el número 19 hexadecimal se vendría destacando con una de las siguientes representaciones:

19h

19_h

Por extraño que nos parezca, este sistema numérico hexadecimal es muy utilizado en el área de las ciencias computacionales. La razón de su enorme utilidad radica en el hecho de que existe una relación sencilla entre las representaciones de un número binario puro y su equivalente en sistema hexadecimal cuando el número binario es un múltiplo de cuatro bits:

aaaaaBinario___Hexadecimal

0000________0
0001________1
0010________2
0011________3
0100________4
0101________5
0110________6
0111________7
1000________8
1001________9
1010________A
1011________B
1100________C
1101________D
1110________E
1111________F

lo cual simplifica enormemente la conversión de un sistema numérico a otro. Por ejemplo, si queremos encontrar el equivalente hexadecimal del siguiente número binario: 

11000101000001101000000101011000

todo lo que tenemos que hacer es "separar" el número binario en grupos de cuatro bits:

1100 0101 0000 0110 1000 0001 0101 1000

tras lo cual podemos convertir directamente cada grupo individual en su equivalente hexadecimal:

C 5 0 6 8 1 5 8

Para convertir un número hexadecimal a binario, simplemente aplicamos el procedimiento inverso. Si queremos convertir el número hexadecimal AF37 a su equivalente binario, lo hacemos tomando en cuenta que A=1010, F=1111, 3=0011 y 7=0111. Así, el número hexadecimal de este ejemplo es igual a:

1010 1111 0011 0111

o en forma más abreviada (aunque un poco menos clara):

1010111100110111

Puesto que se requiere de muchos bits para poder representar un número de tamaño moderado, al leer un número de 32 bits almacenado en un registro como el siguiente:

1010 1111 0101 0111 0110 0001 0001 1011

es mucho más rápido y fácil para un humano escribir o leer:

AF57611B

que el número binario mostrado.

Al igual que en la numeración decimal existen y se manejan con frecuencia los números negativos, precedidos por un signo menos (-) puesto a la izquierda de los mismos, en la numeración binaria también existen y se manejan con frecuencia los números negativos. Sin embargo, en la numeración binaria para distinguir un número negativo de uno positivo no se acostumbra hacerlo con un signo de menos (-). Una forma de llevar a cabo algún tipo de distinción es antecediendo la cifra binaria con un "0" si la cifra es positiva (+) ó con un "1" si la cifra es negativa (-). Si reservamos el primer bit hacia la izquierda para representar el signo del número binario, entonces los siete bits restantes en una palabra binaria de un "byte" no son suficientes para codificar números decimales con suficiente precisión, y en tal caso se requieren por lo menos dos bytes para poder representar números decimales hasta 32 mil. Bajo la convención universal del signo que acabamos de dar:

00000001 representa al número decimal 1

10000010 representa al número decimal -2

Una desventaja de esta representación es que los números binarios de signos distintos no pueden sumados en la forma usual como se acostumbra hacerlo, ya que si sumamos los dos números binarios anteriores el resultado será 10000011, o sea -3, lo cual es incorrecto (la respuesta correcta debería ser -1). De cualquier modo, mantendremos esta representación hasta que encontremos en capítulos posteriores otra que nos permita llevar a cabo en forma correcta operaciones aritméticas con números de signos distintos en el sistema binario obteniendo siempre la magnitud correcta con el signo correcto. De cualquier modo, lo que no cambiará será el uso del primer bit reservándolo para denotar el signo de la cantidad.

Hemos hablado del uso de la numeración binaria para poder ir contando números enteros de uno en uno en el sistema base-2. Es posible que aquí haya algún lector que se pregunte: ¿será posible utilizar también el sistema binario para contar y medir fracciones, cantidades menores que la unidad, tal y como lo hacemos en el sistema decimal? La respuesta es afirmativa, y para poder lograrlo tenemos que introducir en la numeración binaria el mismo artificio que usamos para distinguir números enteros de números menores que la unidad: el punto, que en este caso en vez de ser el punto decimal será el punto binario.

Una fracción representa una división. Al igual que como ocurre en el sistema decimal, las fracciones en el sistema binario pueden ser escritas con un numerador y un denominador separados con una barrita horizontal:

En el sistema decimal las fracciones pueden ser escritas con un punto decimal. Ejemplo de ello son:

Del mismo modo, las fracciones en el sistema binario también pueden ser escritas utilizando un punto para ello, aunque en lugar de hablar de un punto decimal estamos hablando de un punto binario. Así:

Dicho de otra manera, para poder representar fracciones en el sistema binario, el principio sigue siendo el mismo. Los símbolos decimales para cantidades fraccionarias son construídos a base de décimas, centésimas (décimas de décimas), milésimas (décimas de décimas de décimas), diezmilésimas, y así sucesivamente. Los símbolos binarios se construyen a base de mitades, mitades de mitades, mitades de mitades de mitades, y así sucesivamente. Esto nos permite construír la siguiente tabla de equivalencias:

y así sucesivamente. Otras fracciones pueden ser representadas como combinaciones de estos números clave que aparecen en la tabla de equivalencias. Así:

.11 = 1/2 + 1/2 = 3/4

.101 = 1/2 + 1/3 = 5/3

Estos resultados los podemos corroborar de la siguiente manera, representando la fracción como el cociente de dos enteros binarios:

.11 = 11/100 = 3/4

.101 = 101/100 = 5/3

Además del sistema de numeración binaria, del sistema BCD, y del sistema hexadecimal, existen otros sistemas numéricos, entre los cuales tiene cierta prominencia el sistema octal o sistema base-8. Para fines comparativos, a continuación se dá un listado de los primeros diez números en su equivalente decimal, su equivalente octal, y su equivalente binario:

El papel que desempeña el sistema octal en el desarrollo de sistemas digitales basados en circuitos binarios tiene que ver con la relación sencilla que existe entre los símbolos binarios y los símbolos octales. Para poder apreciar mejor esta relación, examínese los siguientes símbolos equivalentes para cantidades un poco mayores:

Para una mejor visualización, cada equivalente binario ha sido separado en grupos de tres dígitos (siguiendo un orden de derecha a izquierda), lo cual nos permite descubrir que cada grupo de tres dígitos se corresponde con el dígito octal equivalente en la misma posición. De este modo, un número binario como 10001001 puede ser separado en grupos de tres dígitos como 10 001 001, lo cual nos permite determinar de inmediato a su equivalente octal como 211. El número binario 10001001 equivale al número decimal 137, y podemos verificar que el número octal 211 también equivale a este número decimal por la táctica usual de asignarle a cada dígito octal su valor posicional en el sistema decimal:

211₈ = 2(8²) + 1(8¹) + 1(8⁰)

211₈ = 2(64) + 1(8) + 1(1)

211₈ = 128 + 8 + 1 = 137₁₀

El propósito de la numeración octal (al igual que la numeración hexadecimal) es tender un puente entre el sistema de numeración decimal que nos es tan familiar y el menos entendible sistema binario. Los símbolos decimales constituyen nuestro medio cotidiano de trabajo para cálculos aritméticos, pero el lenguaje de "unos" y "ceros" es el lenguaje natural con el cual trabajan las máquinas. La desventaja de los números binarios es que se requiere una serie larga de "unos" y "ceros" para poder representar una cantidad que en el sistema decimal se puede representar de manera más compacta, como el número 10001001 que equivale al número decimal 137. La ventaja de utilizar símbolos octales es que son abreviaturas convenientes de símbolos binarios, y el utilizar números octales en lugar de los más familiares números decimales representa un paso natural para acortar la distancia que separa a una computadora "humana" acostumbrada a trabajar en el sistema decimal y la máquina.

1: Problemas resueltos

Problema: Escribir un conteo normal de 20 objetos usando el sistema numérico base 4.

Problema: ¿A cuánto equivale el número 13 decimal en sistema numérico base 6?

El número 13 en sistema decimal equivale al número 21 en sistema base 6. Simbólicamente:

13₁₀ = 21₆

Problema: Convertir el número 20 al sistema base 4 usando el método de división sucesiva.

Aplicando el método de la división sucesiva, tenemos lo siguiente:

La equivalencia del número decimal 20 a su correspondiente 1104 en el sistema base 4 se puede representar de la siguiente manera:

20₁₀ = 110₄

Obsérvese cómo para convertir el número 20 decimal al número 110 en sistema base 4, dividimos primero el número (20) entre la base (4) destacando el primer residuo (0). El cociente de la primera división (5) se vuelve a dividir entre la base (4) agregando agregando el residuo de la segunda división (1) al residuo de la primera (0) para ir formando el número. Puesto que el segundo cociente (1) ya no se puede dividir entre 4, con el segundo cociente (1), el segundo residuo (1) y el primer residuo (0) formamos el número 110 en el sistema numérico base 4.

Problema: Convertir el número 19 al sistema base 2 usando el método de la división sucesiva.

Procedemos del mismo modo que en el problema anterior:

Simbólicamente, podemos expresar el resultado de la manera siguiente:

19₁₀ = 10011₂

Problema: Convertir el número 49 al sistema base 3 usando el método de la división sucesiva y comprobar el resultado haciendo una tabla.

Simbólicamente, podemos expresar el resultado de la manera siguiente:

49₁₀ = 1211₃

La tabla completa de equivalencias hasta llegar al número deseado, en la cual se ha destacado en color ciano la numeración ascendente en sistema decimal, es la siguiente:

Obviamente, resulta mucho más cómodo inclusive para números medianamente pequeños recurrir al método de la división sucesiva que tratar de llegar a un equivalente en otra base numérica mediante la construcción de una tabla.

PROBLEMA: Transformanndo los números decimales 13 y 25 en sus equivalente binarios, sumar dichos números tanto en el sistema decimal como en el sistema binario, poniendo ambas resoluciones la una junto a la otra con el fin de comparar las similitude. Tras esto, conviértase la respuesta binaria a su equivalente decimal usando la tabla de potencias de 2 con el fin de checar la respuesta obtenida de la adición binaria.

Primero se llevará a cabo la "descomposición" de los números 13 y 25 en sus equivalentes en el sistema base 2:

A continuación, se llevará a cabo la suma de los números decimales 13 y 25, junto con la suma binaria de los números 1101 y 11001:

En la suma decimal, para sumar 25 y 13 en la forma en la que estamos acostumbrados, acumulando la respuesta de derecha a izquierda, primero decimos "5 más 3 es igual a 8". En este caso, como la suma parcial no excede de 10, no "llevamos" una unidad para ser sumada a las decenas. El siguiente dígito lo obtenemos diciendo "2 más 1 es igual a 3". Con esto, tenemos el resultado mostrado arriba, que es 38. Veamos ahora cómo se llevó a cabo la suma binaria. Para llevar a cabo la suma binaria, procedemos exactamente de la misma manera, empezando de izquierda a derecha decimos "uno más uno es igual a 10" (recuérdese que en el sistema binario, no existe un símbolo para representar el número 2). Anotamos el cero abajo (puesto en color amarillo) y decimos "anotamos cero y llevamos uno". En la siguiente columna de dígitos, procediendo de izquierda a derecha al igual que como lo hacemos en el sistema decimal, decimos "cero más cero es igual a cero, más el uno que llevábamos es igual a uno". Anotamos este uno a la izquierda del cero que habíamos escrito antes, con lo cual tenemos ya un resultado cumulativo de "10" en color amarillo, procediendo a la siguiente columna de dígitos en donde decimos: "cero más uno es igual a uno, y como no traíamos nada de la adición anterior, anotamos éste uno". Tenemos ya una respuesta cumulativa de "110". Nos vamos a la siguiente columna de dígitos en donde decimos: "uno más uno es igual a 10, y como no traíamos nada de la adición anterior, anotamos cero y llevamos uno". Nuestra respuesta cumulativa lee ya "0110". Así llegamos a la última columna a la izquierda, en donde tenemos únicamente el "1" con el cual decimos "tenemos uno, más el uno que traíamos de la adición anterior, es igual a 10, y como ya no hay más dígitos para sumar, anotamos este 10 para concluír la adición binaria". De este modo, el resultado de la suma binaria es igual al número binario:

100110

Con el fin de checar nuestra respuesta, el equivalente decimal de este número de acuerdo con la tabla de potencias de 2 resulta ser:

100110₂ = (1)2⁵ + (0)2⁴ + (0)2³ + (1)2² + (1)2¹ + (0)2⁰

100110₂ = 32 +0 + 0 + 4 + 2 + 0

100110₂ = 38₁₀

PROBLEMA: Sumar los cuatro números binarios cuyas representaciones hexadecimales son 25h, 62h, 3Fh y 52h.

Los cuatro números hexadecimales, convertidos a la representación binaria, son:

25h = 0010 0101

62h = 0110 0010

3Fh = 0011 1111

52h = 0101 0010

La suma de estos cuatro números se muestra a continuación:

El resultado de la suma, 100011000, se puede representar tambié como su equivalente hexadecimal 118h.

PROBLEMA: Multiplicar los números 13 y 25 convirtiendo cada uno a simbolismo binario, multiplicando las cifras binarias obtenidas, y llevando a cabo la conversión del resultado obtenido a simbolismo decimal.

Los equivalentes binarios de los números decimales 13 y 25 ya fueron obtenidos en el problema anterior, resultando ser 1101 y 11001. Con esto, podemos llevar a cabo la multiplicación en forma similar a como se lleva a cabo en el sistema decimal al cual estamos acostumbrados:

Obsérvese que llevar a cabo una multiplicación binaria pura es mucho más fácil de lo que parece ser a primera vista, ya que en realidad sólo se requiere estar llevando a cabo adiciones sucesivas del multiplicando de acuerdo con el valor que tenga cada uno de los dígitos binarios del número que sea escogido como multiplicador. Si aumentamos la capacidad de bits, podemos estar llevando a cabo multiplicaciones de números realmente grandes sin mayor inversión intelectual que la que ya hemos hecho, y esta multiplicación se llevará a cabo a una rapidez electrónica. ¡No en vano desde hace más de un siglo los inventores humanos se esforzaron por crear máquinas que pudieran llevar a cabo este tipo de operaciones aritméticas a velocidades admirables!

Puesto que el producto de los números decimales 13 y 25 es el número 325, podemos checar nuestra respuesta convirtiendo el número binario obtenido a su equivalente decimal, el cual debe ser también 325. El procedimiento para ello se muestra a continuación:

101000101₂ = (1)2⁸ + (0)2⁷ + (1)2⁶ + (0)2⁵ + (0)2⁴ + (0)2³ + (1)2² + (0)2¹ + (1)2⁰

101000101₂ = 256 + 64 + 0 + 0 + 0 + 0 + 4 + 0 + 1

101000101₂ = 325₁₀

PROBLEMA: Representar en el sistema BCD los siguientes números:

A) 50123
B) 37
C) 4856
D) 102
E) 3971
F) 74
G) 95437

La representación en el sistema BCD de los números indicados se muestra a continuación:

PROBLEMA: Una microcomputadora tiene una capacidad de 16 bits. ¿Cuál es el número más grande que se puede representar bajo esta capacidad en la misma:A) usando el sistema binario, yB) usando el sistema BCD? Comparar la diferencia entre ambos casos.

A) Usando el sistema binario, el número más grande que se puede representar con 16 bits es:

1111111111111111

Este número binario equivale al número decimal:

2¹⁶ - 1 = 65,536 -1

= 65,535

B) Usando el sistema BCD, el número más grande que se puede representar con 16 bits es:

1001__1001__1001__1001

9_____9_____9_____9

o sea, el número 9,999.

Al usar el sistema BCD en lugar del sistema binario, tenemos una diferencia de 65,535-9,999 = 55,536. En otros tiempos en los que los costos para representar cada dígito se medía en términos de bulbos electrónicos y relevadores electromecánicos en lugar de las decenas de miles de transistores microminiaturizados que tenemos en la actualidad, esto se consideraba una pérdida lastimosa de capacidad. De cualquier modo, en nuestros tiempos existen muchas situaciones en las cuales el uso del sistema BCD es una necesidad para proporcionar información más "humana" que sea entendible para la gente ordinaria, ya sea en los relojes digitales, en las carátulas digitales en los hornos de microondas, y en los multímetros digitales que usan los técnicos para medir voltajes y corrientes eléctricas. En estas situaciones, el uso de información binaria pura sería casi indescifrable para los humanos, aunque sea el "lenguaje natural" de la electrónica digital.

PROBLEMA: Convertir el número binario .10101 a su equivalente en sistema decimal.

Usando la tabla de equivalencias descrita en el texto, tenemos que:

.10101 = .10000 + .00100 + .00001

.10101 = 1/2 + 1/8 + 1/32

.10101 = .5 + 125 + .03125

.10101₂ = .65625₁₀

Pero podemos obtener el mismo resultado de la otra manera alterna, la cual consiste en expresar el número binario como una fracción de dos binarios enteros tras lo cual convertimos tanto el numerador como el denominador a su equivalente decimal para así llevar a cabo finalmente la división:

.10101 = 10101/100000

.10101 = (10000 + 100 + 1)/100000

.10101 = (16 + 4 + 1)/32

.10101 = 21/32

.10101₂ = .65625₁₀

confirmando así el resultado obtenido previamente.

PROBLEMA: Convertir el número 110.011 del sistema binario al sistema decimal.

Para convertir este número binario "mixto" que tiene una parte entera y una parte fraccional, basta con darle a cada "1" binario el valor que le corresponde:

110.011 = 100 + 10 + .01 + .001

110.011 = 4 + 2 + 1/10 + 1/100

110.011 = 4 + 2 + 1/4 + 1/8

110.011 = 6 + .25 + .125

110.011₂ = 6.375₁₀

En la forma alterna de solución, expresamos el número como una fracción de dos binarios enteros tras lo cual convertimos tanto el numerador como el denominador a su equivalente decimal llevando a cabo la división:

110.011 = 110011/1000 = (100000 + 10000 + 10 + 11)/1000

110011 = (32 +16 + 2 + 1)/8

110011 = 51/8

110011₂ = 6.375₁₀

confirmando así el resultado obtenido previamente.

PROBLEMA: Convertir las siguientes fracciones binarias a su equivalente decimal, expresando los resultados como números racionales (el cociente de dos números enteros):

a) .011
b) .111
c) .1001
d) .1101
e) .10001
f) .11001

a) Usando la tabla de equivalencias, y procediendo de la misma forma en todos los casos:

.011 = .01 + .001 = 1/4 + 1/8 = 2/8 + 1/8 = 3/8

b)

.111 = .1 + .01 + .001 = 1/2 + 1/4 + 1/8 = 4/8 + 2/8 + 1/8 = 7/8

c)

.1001 = .1 + .0001 = 1/2 + 1/16 = 8/16 + 1/16 = 9/16

d)

.1101 = .1 + .01 + .0001 = 1/2 + 1/4 + 1/16 = 8/16 + 4/16 + 1/16 = 13/16

e)

.10001 = .1 + .00001 = 1/2 + 1/32 = 16/32 + 1/32 = 17/32

f)

.11001 = .1 + .01 + .00001 = 1/2 + 1/4 + 1/32 = 16/32 + 8/32 + 1/32 = 25/32

PROBLEMA: Representar los siguientes números decimales en su equivalente binario, redondeando en donde sea necesario a tres cifras significativas.

a) 2/3
b) 1/5
c) 15/16

a) Primero llevamos a cabo la división para convertir el número expresado en forma de quebrado a su forma decimal:

2/3 = .6666666666...

A continuación redondeamos este resultado a tres cifras significativas:

2/3 = .667

Para encontrar el equivalente binario de esta fracción decimal, podemos llevar a cabo una secuencia de substracciones sucesivas consultando la tabla de equivalencias, lo cual nos produce la siguiente serie de pasos:

.667 - .5 = .167 (Un dígito del equivalente binario será .5 = 1/2 = .10000)

.167 - .125 = .042 (Un dígito del equivalente binario será .125 = .00100)

.042 - .03125 = .01075 (Un dígito del equivalente binario será .03125 = .00001)

Analicemos bien lo que se acaba de realizar: consultando la tabla de equivalencias encontramos que el número decimal fraccionario que se corresponde directamente con un equivalente binario exacto que sea el más grande de todos ellos sin exceder al número decimal .667 es el número .5 que equivale al .1 binario. Anotando esto como resultado parcial y tras llevar a cabo la resta del número decimal .5 del número .667, nos queda el número .167, con lo cual consultamos de nuevo la tabla de equivalencias para encontrar el número decimal fraccionario que se corresponde directamente con un equivalente binario exacto que sea el más grande de todos ellos sin exceder al número decimal .167, que resulta ser el número .125 que equivale al .001 binario, anotando esto como resultado parcial. La respuesta estará dada por la suma de los resultados parciales. Este proceso puede ser repetido mecánicamente cuantas veces queramos, aproximando cada vez con mayor precisión al número decimal fraccionario original.

Así, la respuesta (aproximada) es:

.10000 + .00100 + .00001 = .10101

b) 1/5 = .20

.2 - .125 = .075 (Un dígito del equivalente binario será .125 = .00100)

.075 - .0625 = .0125 (Un dígito del equivalente binario será .00010)

Puesto que .03125 excede a .0125, no podemos restarlo de .0125, con lo cual sabemos que el siguiente dígito significativo en el acumulamiento de los resultados parciales deberá ser un "0". Entonces la respuesta (aproximada) debe ser:

.00100 + .00010 + .00000 = .00110

c) 15/16 = .938 (redondeado a tres cifras significativas)

.938 - .5 = .438 (Un dígito del equivalente binario será .5 = 1/2 = .10000)

.438 - .25 = .188 (Un dígito del equivalente binario será .25 = .01000)

.188 - .125 = .063 (Un dígito del equivalente binario será .125 = .00100)

.063 - .0625 = .0005 (Un dígito del equivalente binario será .0625 = .00010)

La respuesta aproximada es entonces:

.100000 + .01000 + .00100 + .00010 = .11110

PROBLEMA: Convertir los siguientes símbolos binarios a su representación octal.

a) 10110
b) 11110
c) 11011
d) 110011
e) 111000
f) 100011
g) 11110000
h) 11001100
i) 10101010

El procedimiento de solución es directo, consistente en separar los números binarios en grupos de tres haciéndolo de derecha a izquierda:

a) 10110 = 10 110 = 26
b) 11110 = 11 110 = 36
c) 11011 = 11 011 = 33
d) 110011 = 110 011 = 63
e) 111000 = 111 000 = 70
f) 100011 = 100 011 = 43
g) 11110000 = 11 110 000 = 360
h) 11001100 = 11 001 100 = 314
i) 10101010 = 10 101 010 = 252

PROBLEMA: Multiplicar los números octales 56 y 45, sin salir para nada del sistema octal.

Para poder llevar a cabo la multiplicación en el sistema octal, en el cual no existe un símbolo para nuestro número "8", resulta conveniente construír una "tabla de multiplicación" octal, la cual se puede construír fácilmente listando en conteo ascendente todos los números octales desde el uno en adelante, y tras ello ir saltando en dicha lista de dos en dos una vez, de dos en dos tres veces, de dos en dos cuatro veces, de dos en dos cinco veces, y así sucesivamente; y tras esto de tres en tres una vez, de tres en tres dos veces, de tres en tres tres veces, de tres en tres cuatro veces, y así sucesivamente, para ir llenando los casilleros de la tabla de multiplicación de dos por dos, dos por tres, dos por cuatro, etc., tres por dos, tres por tres, tres por cuatro, etc., y así sucesivamente, hasta tener la tabla completa, la cual resulta ser:

Con la tabla de multiplicación octal a la mano, y teniendo siempre en mente la manera en la cual se debe llevar a cabo una suma octal, tomando el número menor (45) como el multiplicador y el número mayor (56) como el multiplicando tal y como se acostumbra en la multiplicación usual, el procedimiento de la operación es el siguiente:

PROBLEMA: Convertir los siguientes números hexadecimales a sus equivalentes en sistema octal.

a) 3A7h
b) 41FBh
c) 7C2Eh
d) D589Ah
e) B0Ce5h
f) 6FF23h

Posiblemente la forma más rápida de llevar a cabo la conversión consiste en convertir directamente cada número hexadecimal a su equivalente binario (base-2) y tras esto reagrupar los dígitos binarios en grupos de tres en tres (de derecha a izquierda) llevando a cabo tras esto la conversión de cada grupo a sistema octal.

a) 3A7h = 0011 1010 0111₂ = 001 110 100 111 = 1647₈

b) 41FBh = 0100 0001 1111 1011₂ = 0 100 000 111 111 011 = 40773₈

c) 7C2Eh = 0111 1100 0010 1110₂ = 0 111 110 000 101 110 = 76056₈

d) D589Ah = 1101 0101 1000 1001 1010₂ = 11 010 101 100 010 011 010 = 3254232₈

e) B0CE5h = 1011 0000 1100 1110 0101₂ = 10 110 000 110 011 100 101 = 2606345₈

f) 6FF23h = 0110 1111 1111 0010 0011₂ = 01 101 111 111 100 100 011 = 1577443₈

2: Las tres funciones lógicas básicas

2: Las tres funciones lógicas básicas

Como parece sugerirlo el ícono puesto arriba al comienzo de todos los capítulos de este libro, existen tres bloques fundamentales con los cuales se pueden construír todas las funciones lógicas capaces de ser concebidas por la mente humana. Estos son los ladrillos sobre los cuales descansan todas las computadoras que se usan hoy en día, desde las computadoras caseras hasta las supercomputadoras más poderosas.

Comenzaremos nuestra introducción al mundo de la lógica digital repasando los principios del funcionamiento de los relevadores electromecánicos, los cuales se apoyan en el bien conocido fenómeno de que cuando se le aplica una corriente eléctrica a un alambre con aislamiento que está enrollado alrededor de un cilindro metálico (o inclusive enrollado alrededor de un clavo ordinario), se crea un campo magnético que puede atraer a otros objetos metálicos, como lo muestran las siguientes figuras:

En la figura de la izquierda, al aplicarle al alambre enrollado en torno al cilindro metálico un voltaje proporcionado quizá por alguna batería, el voltaje produce una corriente eléctrica la cual a su vez crea un campo magnético, cuyas "líneas de fuerza" magnéticas pueden actuar sobre objetos metálicos cercanos a ellas. Y en la figura de la derecha, al remover el voltaje, el campo magnético desaparece. Encima de ambas figuras se ha dibujado una laminita metálica móvil que actúa como interruptor eléctrico o switch, la cual está unida a un resorte (no dibujado) que la jala hacia arriba. Como puede verse, al aplicarse un voltaje al alambre enrollado, el interruptor eléctrico se cierra, estando habilitado para permitir el paso de la corriente eléctrica, mientras que al no haber voltaje, por la acción del resorte que jala a la laminita hacia arriba el contacto se rompe. Para simplificar nuestro análisis, al voltaje que le aplicamos al alambre, que puede ser de 1.5 volts, 9 volts, o algún otro valor, lo llamaremos simplemente como "1" (uno). Y a la ausencia de dicho voltaje la llamaremos simplemente como "0" (cero). De este modo, al aplicarle un "1" al relevador, el contacto eléctrico puesto encima del mismo se cierra, y al remover dicho "1" (que es lo mismo que aplicar un "0"), el contacto eléctrico se abre. Puesto que las terminales de conducción eléctrica del alambre enrollado (al cual llamaremos bobina) son eléctricamente independientes (aisladas) de las terminales de conducción eléctrica que se unen por la acción de la laminita puesta encima de la bobina, el valor que tome la entrada de voltaje a la bobina del relevador, ya sea "0" ó "1", no será afectado por lo que suceda a la salida del mismo, llamándosele aquí "salida" a cualquier señal de voltaje que pueda ser transmitida por la laminita superior al ser cerrada por la acción del campo magnético del relevador activado con un "1".

A continuación, por cortesía del sitio HowStuffWorks.com, tenemos un archivo animado que muestra cómo trabaja un relevador electromecánico al cerrarse el interruptor que permite que la bobina del relevador sea energizada por una batería, permitiendo con ello que se cierre el circuito para que otra batería pueda encender un foco (ampliar imagen para poder ver la animación en acción):

Aunque la batería (fuente de poder) que energiza a la bobina del relevador es una y la batería que enciende al foco es otra, la figura sugiere que se trata de baterías iguales proporcionando el mismo nivel de voltaje (por ejemplo, 5 volts) tanto a la bobina del relevador como al foco, lo cual sugiere que en lugar de tener que utilizarse dos baterías se podría utilizar una sola batería, la misma batería actuando en común para ambos propósitos. Esto es importante porque el "1" que activa al relevador vendría a ser en todos sentidos el mismo "1" que enciende al foco. Considérese a continuación el siguiente circuito formado por dos relevadores, en los cuales los resortes que normalmente jalan las palancas (o laminitas) conectoras de los relevadores son mostrados de color rojo:

Normalmente, toda fuente de corriente directa como los acumuladores de los automóviles tiene un polo positivo (+) y un polo negativo (-), pero con fines de simplificación en los diagramas y esquemáticos se acostumbra designar al polo negativo (-) como tierra eléctrica (en inglés, ground ó GND). Esto nos permite "olvidarnos" del polo negativo y hablar simplemente de la aplicación de un "1" (un voltaje) o de un "0" (ningún voltaje) a una terminal como la terminal A ó como la terminal B. En este diagrama, si aplicamos un voltaje positivo (que aquí también llamaremos simplemente "1") en la terminal A, el relevador se energizará. Obsérvese que en un contacto conector superior del relevador izquierdo tenemos un voltaje de +6 volts, el cual al ser activada la terminal A con un voltaje de "1" y cerrarse la conexión superior del relevador puede pasar a la otra terminal del mismo. Sin embargo, este voltaje no llegará hasta el extremo izquierdo de la configuración, designado como Q, si la entrada del relevador del lado derecho no ha sido activado también en su terminal B con un "0", por estar conectadas las terminales de contactos de ambos relevadores en serie, una tras la otra. La única manera en la cual el voltaje de +6 volts puede llegar desde el lado izquierdo de la configuración hasta el lado derecho en la terminal Q es si ambos relevadores están energizados con un "1" en las terminales A y B. Supongamos por un momento que hemos diseñado aquí los relevadores de modo tal que el voltaje requerido para energizar cualquiera de ellos sea también de +6 volts. Esto nos permite llamar a los +6 volts simplemente como "1". Y nos permite hacer una afirmación interesante: si las entradas en las terminales A y B son "1", entonces la salida Q también será "1". Pero si cualquiera de las entradas en las terminales A y B o en ambas es "0", entonces la salida será "0". Unicamente cuando ambas entradas son "1" tendremos una salida de "1". Unicamente cuando A y B son ambas "1" la salida será también "1".

Podemos representar el funcionamiento de este tipo de circuito de una manera más concreta y más fácil de leer:

La traducción inglesa de la palabra española "y" es la palabra and. Esta es precisamente la palabra que usaremos para identificar cualquier tipo de sistema combinado que muestre un comportamiento como el que acabamos de ver. Es común representar un circuito de esta naturaleza de la manera siguiente:

Este bloque es mejor conocido como la función AND que como ya se dijo su traducción del inglés al español significa la palabra "y", como en la frase "patria y libertad", y es en sí una función lógica básica. Este será uno de nuestros "ladrillos" fundamentales. Podemos representar sus propiedades en una tabla mejor conocida como Tabla de Verdad que se muestra a continuación:

Considérese ahora el siguiente circuito construído con relevadores electromecánicos:

Si no hay voltaje alguno aplicado en las dos terminales de entrada A y B, las bobinas de ambos relevadores no se energizarán y los dos interruptores de ambos relevadores se mantendrán en las posiciones mostradas en el diagrama. En tal caso, el voltaje (+) que llamaremos "1" no llegará a la Salida, no habiendo por lo tanto voltaje alguno en ella. La ausencia de voltaje en la Salida la identificaremos con un "cero" ó "0". La situación cambia cuando aplicamos un voltaje (o un "1") en la terminal A, en tal caso la bobina se energiza y "jala" el contacto hacia abajo, conectando el voltaje (+) a la Salida, con lo cual la Salida pasará de la condición "0" a la condición "1". Este "1" permanecerá en la Salida mientras haya un "1" aplicado en la terminal "1". Por otro lado, cuando aplicamos un voltaje (o un "1") en la terminal B, en tal caso la bobina también se energizará y "jalará" el contacto hacia abajo, conectando el voltaje (+) a la Salida, con lo cual la Salida pasará de la condición "0" a la condición "1". Y si ambas terminales de entrada A y B son energizadas con un "1", la Salida seguirá recibiendo el voltaje (+) ó "1" por las dos vías. Básicamente, tenemos un circuito en el cual la Salida será "1" cuando cualquiera de las entradas A ó B tenga un "1" aplicado en ella.

La traducción inglesa de la palabra española "o" es la palabra or. Esta es precisamente la palabra que usaremos para identificar cualquier tipo de sistema combinado que muestre un comportamiento como el que acabamos de ver. Es común representar un circuito de esta naturaleza de la manera siguiente:

Este bloque es mejor conocido como la función OR que como ya se dijo su traducción del inglés al español significa la palabra "o", como en la frase "patria o muerte", y es en sí otra función lógica básica. Este será otro de nuestros "ladrillos" fundamentales. También podemos representar sus propiedades en una Tabla de Verdad como la que se muestra a continuación:

Aquí podemos ver el sentido de la palabra OR. La salida del circuito será 1 si la entrada A o la entrada B tienen un valor de 1.

Por último, consideremos ahora el siguiente circuito construído con un solo relevador electromecánico sencillo, en el cual cuando no hay voltaje alguno aplicado a la terminal de entrada A (lo cual equivale a poner cero volts o "0" en la terminal de entrada), el voltaje positivo (+) que designamos como "1" lógico pasa directamente a la Salida:

Supóngase ahora que se le aplica un voltaje (un "1") a la terminal de entrada A. Al energizarse la bobina del relevador, al convertirse en un imán por la acción de la corriente eléctrica "jalando" con ello el interruptor encima de él hacia abajo , el contacto superior que conectaba la Salida a una fuente de voltaje positivo (un "1") desciende de su posición normal, desconectando dicha terminal del voltaje positivo, lo cual equivale a dejar sin voltaje alguno la Salida, lo cual podemos tomar como un "cero" ("0") lógico. Prescindiendo de los detalles innecesarios, tenemos un componente en el cual cuando la entrada es "0" la salida es "1", y cuando la entrada es "1" la salida cae a "0". Esto es lo que llamamos comúnmente como una inversión lógica. Este componente es por lo tanto un inversor.

Es común representar simbólicamente un componente que funcione de esta manera en la siguiente forma:

Es importante aclarar que lo que realmente representa la función inversora es la "burbuja" colocada a la derecha del triángulo. El triángulo en sí, históricamente, pretendía hacer notar que además de la inversión se estaba llevando a cabo una amplificación elétrica de la señal para corregir cualquier deterioro previo que hubiera tenido, y de hecho el símbolo sin la burbuja es conocido como buffer, aunque el buffer en sí no lleva a cabo ningún procesamiento de información porque un "0" puesto a su entrada pasa como un "0" a su salida y un "1" puesto a su entrada también pasa inalterado como un "1" a su salida. Es común en muchos circuitos lógicos utilizar únicamente la burbuja ya sea en una o varias de las entradas y/o en una o varias de las salidas para indicar que en ese punto se está llevando a cabo una inversión. Es importante aclarar que, por lo general, la burbuja sólo tiene este significado únicamente cuando está "pegada" a una de las funciones lógicas básicas o a algún componente derivado de la misma.

El bloque simbólico arriba mostrado es mejor conocido como la función NOT (palabra que proviene de la palabra inglesa not que en español significa "no", como en la frase de negación "carlos no es un arquitecto") y es nuestra tercera función lógica básica. Podemos resumir sus propiedades en la siguiente Tabla de Verdad:

Estos son los únicos bloques que necesitamos para construír cualquier computadora capaz de correr un programa como Windows o Linux. Se necesitan muchos de ellos para poder armar una computadora, claro está, pero la gran integración de millones de transistores en un pequeños circuitos integrados de elevada densidad permite lograr la construcción de super-computadoras que todavía hace apenas dos décadas se habrían antojado imposibles de lograr. Las tecnologías de manufactura han sido diversas, desde los primitivos relevadores electromecánicos con los cuales IBM construyó la computadora Harvard Mark I en 1944 en los Estados Unidos a iniciativa del Doctor Howard Aiken, y con los cuales Konrad Zuse construyó la computadora Z3 en 1941 en Alemania, pasando por los bulbos electrónicos al vacío (anteriormente utilizados para la construcción de radios y televisores "primitivos") con los cuales se construyó la computadora ENIAC, hasta llegar a los transistores y los circuitos integrados que permitieron la construcción de microcomputadoras y minicomputadoras, culminando con los primeros microprocesadores que empezaron a ser fabricados por Motorola e Intel que permitieron la fabricación de computadoras caseras como la que tiene el lector precisamente en estos momentos en sus manos. Sin embargo, detrás de todas las variantes tecnológicas, una cosa no ha cambiado, y esto es la teoría fundamental que las hace operar, basada siempre a fin de cuentas en tan sólo tres funciones lógicas básicas, el bloque OR, el bloque AND y el bloque NOT.

Las funciones lógicas OR y AND pueden tener no solo dos sino tres o más entradas cada una. Analicemos, por ejemplo, un AND de tres entradas:

Puesto que en el AND de dos entradas la salida es 1 únicamente cuando todas sus entradas son 1, extendiendo la definición tenemos que en el AND de tres entradas la salida también será 1 únicamente cuando todas las entradas sean 1. Teniendo esto en mente, podemos construír inmediatamente una Tabla de Verdad para el AND de tres entradas:

Del mismo modo, podemos hacer una extensión similar del concepto del bloque OR para un OR que tenga más de dos entradas, en donde extendiendo la definición tenemos que la salida de un OR con cualquier número de entradas será 1 cuando cualquiera de las entradas o una combinación de cualquiera de las entradas tenga un valor de 1.

Estudiemos ahora lo que ocurre cuando conectamos un OR a un NOT de la manera siguiente:

Aplicando todas las combinaciones posibles de unos y ceros en las entradas, obtenemos la salida para cada combinación posible tomando tomano en cuenta las propiedades del OR y la acción inversora del NOT, con lo cual podemos construír la siguiente Tabla de Verdad:

Tenemos un circuito que produce un 1 a la salida únicamente cuando ambas entradas son 0. Esta configuración es mejor conocida como la función NOR (la palabra NOR es una contracción de las palabras NOT-OR, que son los elementos usados para construír esta configuración) y se representa de la siguiente manera:

A continuación estudiemos lo que ocurre cuando conectamos un AND a un NOT de la manera siguiente:

La Tabla de Verdad para este circuito deberá ser como se muestra a continuación:

Tenemos un circuito que produce un 0 a la salida únicamente cuando ambas entradas son 1. Esta configuración es mejor conocida como la función NAND (la palabra NAND es una contracción de las palabras NOT-AND, que son los elementos usados para construír esta configuración) y se representa de la siguiente manera:

Las funciones NOR y NAND son ejemplos claros que muestran cómo se pueden utilizar las tres funciones lógicas básicas para construír funciones más complejas.

Estudiemos ahora la siguiente situación:

La pregunta que nos hacemos es la siguiente: ¿Cuál será la salida del OR al introducir las palabras 01100 y 11001 en sus entradas?

Para responder a esta pregunta, notamos que los primeros bits en entrar al OR son el último bit de la palabra 01100 (esto es, un 0) y el último bit de la palabra 11001 (esto es, un 1). La salida producida por el OR será por lo tanto un 1. A continuación, los siguientes bits que entran son el penúltimo bit de la palabra 01100 (esto es, un 0) y el penúltimo bit de la palabra 11001 (esto es, un 0). La siguiente salida producida por el OR será por lo tanto 0, con lo cual a su salida ya se habrá formado la palabra 01. De esta manera, vemos que a su salida se formará la siguiente palabra:

11101

Puesto que la palabra en la salida del OR es diferente de las palabras a sus entradas, decimos que se ha llevado a cabo un procesamiento de información. Este es el propósito fundamental de todos los circuitos lógicos.

Supongamos ahora que se nos presenta un componente electrónico en el cual los niveles de voltaje naturales al sistema son +5 volts y 0 volts. Dicho componente electrónico tiene dos terminales de entrada A y B y una terminal de salida. Al aplicar los siguientes niveles en sus entradas produce los siguientes niveles de voltaje en su salida:

Designando al voltaje mayor (o más positivo) de +5 volts como "1" y al voltaje menor (o más negativo) como "0", la Tabla de Verdad toma el siguiente aspecto:

El circuito se comporta como una función OR.

En este último ejemplo, muy bien podríamos haber adoptado otra convención igualmente válida. Podríamos haber identificado al voltaje de +5 volts con un "0" y al voltaje de cero volts con un "1", lo cual nos produce otra Tabla de Verdad diferente. Esto es lo que se conoce como lógica negativa. Con el propósito de evitar confusiones, nos hemos abstenido y nos seguiremos absteniendo de utilizar este enfoque, aunque una vez que se hayan dominado los principios la lógica positiva y la lógica negativa son tan válidas la una como la otra. Hagamos al menos con este ejemplo tal cosa; construyamos la Tabla de Verdad asignándole al nivel de +5 volts un valor lógico de "0" y al voltaje de cero volts un valor lógico de "1". Entonces la Tabla de Verdad que se obtiene será la siguiente:

El circuito se comporta como una función AND.

Tenemos entonces que el comportamiento lógico de un circuito dependerá de las asignaciones que le demos a sus niveles de voltaje. La práctica de designar al voltaje mayor (o más positivo) como "1" y al voltaje menor (o más negativo) como "0" es conocida como lógica positiva. La práctica de designar al voltaje menor (o más negativo) como "1" y al voltaje mayor (o más positivo) como "0" es conocida como lógica negativa.

En el resto de esta obra, a menos que se indique lo contrario, se utilizará exclusivamente lógica positiva.

Con las tres funciones lógicas básicas podemos construír circuitos más elaborados, de creciente complejidad, cuyo análisis se puede llevar a cabo suponiendo todas las combinaciones posibles de "unos" y "ceros" a la entrada, y siguiendo el flujo de cada combinación de valores para ver lo que tenemos a la salida podemos comprobar la función desempeñada por el circuito. Por convención, los diagramas de circuitos lógicos se dibujan de modo tal que el flujo de señales es rastreado de izquieda a derecha. A continuación tenemos el diagrama de un circuito lógico simple en cuyas dos terminales de entrada a y b se han puesto dos "unos" ("1"):

En el AND que tenemos en el extremo izquierdo del diagrama, tenemos dos unos ("1") a la entrada, los cuales producen un "1" a la salida del mismo. Este "1" a la salida del AND es invertido por el NOT, convirtiéndose en un "0". De este modo, tenemos a las entradas del OR en el extremo derecho del diagrama un "0" y un "1", los cuales producen un "1" a la salida del mismo. Nos falta por comprobar otras combinaciones de valores restantes, las cuales son a=0 y b=0, a=1 y b=0, a=0 y b=1. Este método de rastreo de valores de señales se puede aplicar a cualquier circuito lógico, por complejo que sea.

Al ir construyendo circuitos lógicos cada vez más complejos, los alambres que van conectados entre sí se mostrarán conectados explícitamente con un "punto" conector, mientras que los alambres que simplemente se cruzan uno por encima del otro sin conectarse no tendrán el punto conector:

Sin embargo, en las junturas tipo "T" en los diagramas esquemáticos:

se sobreentenderá que siempre hay una conexión entre los dos alambres, ya sea con o sin la presencia del "punto" conector (en esto hay que tener cierta precaución, ya que en los simuladores de circuitos lógicos en una gran variedad de programas computacionales es indispensable agregar siempre en los diagramas de simulación el "punto" conector, ya que muchos de estos programas no están preparados para reconocer esta convención)

En el diseño de circuitos lógicos, una de las cosas que no está permitida es conectar directamente a un mismo punto la salida de dos funciones lógicas en una forma como la que se muestra a continuación:

Puesto que se ha definido el "1" como el polo positivo de la fuente de poder (por ejemplo, +5 volts) y el "0" como el polo negativo de la misma fuente de poder (conocida vulgarmente como "tierra eléctrica"), la situación mostrada mostrada equivale ni más ni menos que a un corto circuito. Y aunque la gran mayoría de los circuitos integrados discretos que se venden en la actualidad tienen integrada en su microelectrónica una estructura de resistencias y transistores que evitan que un corto circuito de esta naturaleza los pueda dañar, limitando el flujo de la corriente a través de los mismos, la salida de un circuito lógico de esta naturaleza es en el mejor de los casos indefinida.

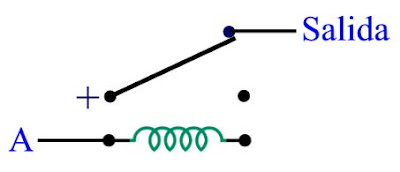
Si por alguna razón insistimos en querer conectar juntas las salidas de dos (o más) funciones lógicas básicas, lo podemos hacer utilizando diodos rectificadores, los cuales conducen corriente eléctrica en una sola dirección más no en la dirección contraria. Físicamente, en un circuito real, estos componentes tienen un aspecto como el que se muestra a continuación, en donde la banda puesta en un extremo del componente indica la polaridad del cátodo (la parte del componente que va conectada al polo negativo de la fuente de poder cuando se desea que este componente conduzca corriente eléctrica), correspondiendo con banda tocada por la flecha en el símbolo representativo del diodo que aparece a la derecha:

Usando diodos rectificadores, el circuito lógico anterior ya "corregido" presentaría el siguiente aspecto:

En este circuito el AND superior está poniendo un "0" en su terminal de salida mientras que el NOT inferior está poniendo un "0" en la suya propia. El voltaje relacionado con el "1" lógico normalmente produce una corriente eléctrica que fluye hacia el "0" lógico. Pero en los diodos rectificadores, la corriente eléctrica solo puede fluír en la dirección que marca la flecha, de modo tal que si en la cola de la flecha hay un "0" y en la punta de la flecha hay un "1" como ocurre con el AND superior, el diodo no permitirá el paso de la corriente y actuará como si el alambre estuviera cortado, efectivamente desconectando al AND de la salida combinada. En otras palabras, el "1" del inversor NOT es el que gana. Pero si la salida del NOT fuese "0" y la salida del AND fuera "1", entonces el AND ganaría. Y si la salida de ambos fuera "1", entonces ambos ponen un "1" lógico en la línea de salida y no hay contradicción lógica alguna (ni corto circuito). Pero si repasamos estas funciones, nos daremos cuenta de que la inserción de los diodos en el circuito hace que entre ambos proporcionen el equivalente de la función OR, con la desventaja de que los diodos no proporcionan ninguna amplificación de la señal. Las buenas prácticas de diseño nos indican remover los dos diodos y reemplazarlos por un bloque OR.

Existe una excepción importante a la prohibición de conectar directamente a un mismo punto las salidas de dos o más bloques lógicos, y ello ocurre cuando se están utilizando circuitos integrados capaces de implementar algo que se conoce como la lógica alambrada (wired logic), también conocida como la lógica de colector abierto (open collector logic), lo cual tiene que ver con el hecho de que tales circuitos, construídos a base de transistores bipolares (un transistor bipolar básico tiene tres terminales, la base, el emisor y el colector), utilizan la terminal denominada "colector" del transistor bipolar en modo "abierto" (sin conexión previa) para llevar a cabo esta función, estando por ello diseñados para conectarse a un mismo punto al cual además hay que agregar una resistencia conectada al polo positivo del voltaje de la fuente de poder, como se muestra en el siguiente esquema en el que se han conectado las salidas de dos bloques NOT:

Por regla general, al utilizarse la lógica alambrada ó "lógica de colector abierto", en el punto de unión se lleva a cabo la función AND; esta es la razón por la cual en el dibujo anterior se bosquejó un AND alrededor del punto de unión de las salidas de los NOTs. Si ponemos un "0" a la entrada de ambos NOTs, la salida de los dos será "1", y por la acción del AND en el punto de juntura la salida Y del circuito tendrá un valor de "1". Si cualquiera de las entradas A ó B a los NOTs es de "1", el cual será invertido a "0", entonces por la acción AND sobre la salida de ambos la salida común Y tendrá un valor de "0". Y si ambas entradas son "1", entonces la salida Y será "0". Tenemos entonces un circuito en el cual la salida será "1" únicamente cuando ambas entradas son "0", lo cual es en efecto la acción de un circuito NOR. El símbolo A·B puesto en el dibujo para representar el valor lógico de la salida Y representa esta acción AND en la simbología del álgebra Boleana, cuya discusión será postpuesta y aclarada en el siguiente capítulo.

No cualquier familia de circuitos lógicos integrados puede conectarse de esta manera. Obsérvese que dentro de los bloques NOTs se dibujó el símbolo de un pequeño diamante con una barra horizontal puesta debajo del mismo. Este es el símbolo utilizado para indicar en los diagramas esquemáticos que se están usando componentes trabajando bajo lógica alambrada, lo cual está especificado por la convención técnica IEEE/ANSI-1984 que indica que cualquier componente cuya salida pueda ser alambrada a otro componente bajo lógica alambrada deberá destacarse dibujando dentro del bloque lógico cerca de la salida del mismo el símbolo del diamante con la barra horizontal puesta debajo del diamante:

Como muestra de esta simbología, a continuación tenemos dos ANDs de colector abierto, de tres entradas cada uno, con sus salidas conectadas directamente dándonos el equivalente de un AND de seis entradas en total:

Para el ejemplo que vimos en donde conectamos directamente las salidas de dos inversores lógicos NOT, posiblemente utilizaríamos como NOTs con lógica de colector abierto los que proporciona un circuito integrado como el 7405, el cual incluye seis inversores NOT y cuya relación de terminales "pins" es la que se muestra a continuación:

A continuación se muestran las salidas de tres NOTs de este circuito integrado conectadas al mismo punto bajo el esquema del "colector abierto":

Algunos otros circuitos integrados cuyo funcionamiento se basa en la "lógica del colector abierto" son el 7403 (el cual proporciona compuertas NAND empleando la misma relación de terminales "pins" que el circuito integrado 7400 que no es de "colector abierto"), el 7409 (el cual proporciona compuertas AND con la misma relación de terminales "pins" que el 7408) y el 7433 (el cual consiste de bloques NOR y tiene la misma relación de terminales "pins" que el 7402).

Para poder llevar a cabo experimentos con circuitos lógicos básicos que hayamos diseñado o cuyo comportamiento queramos verificar, tenemos dos alternativas. La primera es construír algún prototipo experimental usando circuitos integrados que se puedan procurar en el mercado. En el mercado han aparecido (y siguen apareciendo) muchos "kits" de bajo costo para facilitarle la labor a los experimentadores. A continuación se muestra uno de los primeros en aparecer en los años setenta gracias al abaratamiento de los circuitos electrónicos integrados, el Digital Logic Microlab, el cual fue vendido por Southwest Technical Products y el cual fue popularizado por algún tiempo por la revista Popular Electronics:

El simulador lógico arriba mostrado implementa su electrónica con una tecnología ya obsoleta que los ingenieros llaman RTL (Resistor Transistor Logic), la cual terminó siendo desplazada por otra tecnología mucho más veloz, llamada TTL (Transistor Transistor Logic). La tecnología RTL usada por este simulador no implementa directamente ninguna de las funciones lógicas básicas aquí estudiadas, ya que su bloque fundamental es el bloque NOR. Si nos fijamos bien en la parte media del simulador, hay cuatro bloques NOR, los cuales son obtenidos de un circuito integrado, el circuito integrado básico de la familia RTL, el 4001. Obsérvese que el NOR es representado en el simulador con un símbolo triangular y "la burbuja de negación lógica" puesta en la punta del símbolo triangular, de acuerdo con lo que se acostumbraba en aquellos días. Si tuviéramos uno de esos simuladores a la mano y lo viéramos en su interior, encontraríamos que los cuatro bloques NOR accesibles para interconexión mediante los postes en la carátula provienen de un circuito integrado que tiene el siguiente aspecto:

Una inspección al diagrama esquemático de este circuito integrado nos muestra en su relación de terminales que efectivamente tiene cuatro bloques NOR en su interior:

A continuación tenemos otro "laboratorio" casero cuyo propósito es ir introduciendo a las nuevas generaciones de técnicos e ingenieros al mundo de la lógica digital, en el cual podemos ver algunas de las funciones lógicas cubiertas dentro de este capítulo así como otras funciones lógicas un poco más elaboradas cuyo estudio se dejará para capítulos posteriores:

Gracias a la potencia de las computadoras de escritorio, existe una alternativa mucho más económica y mucho más rápida para "construír" un prototipo utilizando varias combinaciones de circuitos lógicos, y esta consiste en usar un simulador de "software", o sea un programa corriendo en la computadora que permita tomar los símbolos lógicos convencionales de un catálogo para irlos "conectando" en el monitor de la computadora. Lo que aquí se hace es llevar a cabo una simulación de un experimento virtual en donde no hay un solo alambre a la vista, todo se lleva a cabo esquemáticamente desde el teclado. Uno de tales simuladores es el simulador lógico Digital Works, el cual tiene un costo aproximado de ochenta dólares:

Existen también simuladores gratuitos de alta potencia que pueden ser descargados gratuitamente de Internet. Uno de ellos es el simulador lógico Logisim, desarrollado en 2002 por Carl Burch, el cual puede correr en cualquier computadora casera que tenga implementada la plataforma Java (hoy la gran mayoría la tiene, y las que no la tienen la pueden obtener también gratuitamente de Internet):

El simulador lógico Logisim se puede descargar gratuitamente del siguiente enlace:

http://ozark.hendrix.edu/~burch/logisim/index_es.html

Otro programa gratuito es el Digital Simulator, desarrollado en 1996 por Iwan van Rienen, , el cual no es un programa ejecutable en el estricto sentido de la palabra, sino que se trata de un applet de la plataforma Java, la cual tiene que ser instalada en la computadora antes de que el Digital Simulator pueda correr. La carpeta fuente conteniendo todos lo necesario para correr el simulador se puede descargar gratuitamente como un archivo comprimido ZIP generalmente titulado DigSim.zip, el cual al ser descomprimido en una carpeta no muestra archivo ejecutable alguno desde donde se pueda "lanzar" el Digital Simulator, ya que lo único que aparecen son las famosas "clases" con las que opera Java. De cualquier modo, suponiendo que la computadora tenga ya instalada la plataforma Java, se puede pulsar rápidamente con el "mouse" de la computadora sobre cualquiera de los archivos que terminen con extensión ".html". Esto hará que se invoque el navegador que tenga instalado la computadora (por ejemplo, Internet Explorer), y al ser invocado el navegador la plataforma Java será invocada por el contenido mismo del archivo ".html" seleccionado, tras lo cual deberá aparecer una ventana como la siguiente (en este caso, se ha escogido la ventana que aparece al pulsar un archivo titulado "sim_and.html", la cual muestra la acción de la función AND con dos interruptores conectados en serie, y la acción del bloque lógico AND):

Una vez que aparece la ventana, es asunto fácil ir seleccionando desde la línea del menú los componentes que queramos ir agregando a un circuito nuevo que queramos "construír" después de haber borrado todo seleccionando desde el menú la opción "File -> New". En la opción titulada "Passive" podemos seleccionar alambres conectores (Wire), un punto de conexión de dos alambres que se cruzan (Junction) para unirlos eléctricamente, el polo positivo de la fuente de poder Vcc (equivalente a nuestro "1" lógico) que aparecerá en el extremo superior izquierdo de la ventana de trabajo, el polo negativo o "tierra" eléctrica (equivalente a nuestro "0" lógico) que también aparecerá en el extremo superior izquierdo, un interruptor (Switch) y un interruptor de botón (Push button) los cuales se pueden "arrastrar" hacia al interior de la ventana manteniendo oprimido el "mouse" de la computadora. En la opción titulada "Ports" podemos seleccionar una de varias compuertas lógicas que también irán apareciendo en el extremo superior izquierdo de la ventana, ya sea un NOT (Inverter), un AND, un OR, o cualquiera de otros bloques. En "bi-stable" podemos seleccionar componentes secuenciales que serán tratados posteriormente en este libro. En la opción "Display" podemos seleccionar diodos emisores de luz LED para poder obtener confirmación visual "lumínica" sobre la presencia de un "0" o de un "1", y en la opción "Special" podemos seleccionar otros componentes más sofisticados tales como un generador de "pulsos" (Oscilator) e inclusive una "punta de prueba lógica" para medir en algún punto de un circuito y saber si tenemos un "0" ó un "1". La acción del simulador puede ser puesta en marcha presionando el "botón" con un relámpago amarillo dibujado dentro del mismo. Y si antes de construír un circuito lógico por cuenta propia el usuario no está seguro de cómo trabaja esta ventana "applet" de Java, puede seleccionar alguno de varios ejemplos incluídos en el paquete con la opción de la línea del menú "File -> Open example". Una cosa que no puede hacer el programa es guardar en la computadora archivos de circuitos diseñados, debido a las medidas de seguridad implementadas por Java.

El Digital Simulator desarrollado por Iwan van Rienen fue actualizado posteriormente con algunas mejoras llevadas a cabo por Deborah E. Lynch y Phil White, y rebautizado con el nombre de Digital WorkShop. En una de sus versiones más comunes, el archivo DigiSim.zip -en el cual esta puesto el Digital Workshop- al ser desempacado produce varias carpetas y un archivo ejecutable, el archivo Java Digisim.jar. Para echar a andar el Digital Workshop, basta con pulsar con el mouse el ícono que representa al archivo Digisim.jar, con lo cual el usuario puede comenzar a "ensamblar" de inmediato circuitos lógicos de todo tipo. Una cosa que descubrirá el usuario es que el Digital Workshop, a diferencia del Digital Simulator, no requiere activar el navegador de la computadora para poder funcionar, puede andar por sí solo (esta es precisamente una de las ventajas de los archivos ejecutables con extensión ".jar"). Puesto que el modo de funcionamiento del Digital Workshop es casi idéntico al modo de funcionamiento del Digital Simulator que se acaba de describir, no será necesario repetir aquí los detalles.

Aún otro programa que se puede descargar gratuitamente, el cual por cierto era algo costoso pero que hoy sus creadores han hecho accesible públicamente al mundo entero de manera gratuita a través de Internet, es el programa MultiMedia Logic, cuya interfaz visual presenta el siguiente aspecto:

Este programa se puede descargar sin costo alguno de varios sitios como el siguiente:

http://www.softronix.com/logic.html

Otra opción extremadamente buena para "construír" circuitos lógicos (simulados) en el monitor de una computadora es la versión estudiantil del programa PSpice, la cual se puede descargar sin costo alguno de la siguiente dirección:

http://www.electronics-lab.com/downloads/schematic/013/

Este programa aún en su versión estudiantil es un programa tan completo y tan sofisticado que el archivo de descarga tiene un tamaño de 28 Megabytes, de modo que la descarga del mismo no es recomendable a través de una conexión Internet de baja velocidad.

Además de los programas anteriormente mencionados que nos permiten diseñar y "construír" circuitos lógicos (simulados), existe otra alternativa inmediata para poder ver la acción de los circuitos lógicos "en vivo" de forma interactiva, como si se tuviese a la mano un tablero con los componentes físicos reales. A modo de ejemplo, se recomienda visitar el siguiente sitio en el cual el usuario puede "jugar" a través del "mouse" de la computadora con varias compuertas lógicas, "encendiendo" con "unos" o "apagando" con "ceros" las terminales de entrada, viendo de inmediato los efectos a la salida (o salidas) de los circuitos lógicos en los diodos emisores de luz (LED) simulados:

http://www.dst-corp.com/James/LogicPrimer/Gates.html

Los circuitos lógicos interactivos que aparecen en este último enlace fueron creados precisamente con el programa MultiMedia Logic ya mencionado.

Otro sitio muy completo, mantenido por la Universidad de Hamburgo en Alemania, proporciona programas que le demuestran al visitante de una manera interactiva visual el comportamiento de los circuitos lógicos que acabamos de ver. En la siguiente dirección:

http://tams-www.informatik.uni-hamburg.de/applets/hades
______/webdemos/10-gates/00-gates/basic.html

podemos "cambiar" las entradas de las compuertas lógicas y ver de inmediato cómo cambia la salida de las mismas.

Aún otro sitio muy interesante de visitar, en el cual el usuario también se puede divertir "jugando" un buen rato con compuertas lógicas simuladas como las que exhibe el enlace anterior, es el siguiente sitio mantenido por el Profesor Constantinos E. Efstathiou, Director del Laboratorio de Química Analítica de la Universidad Nacional y Kapodristiana de Atenas:

http://www.dst-corp.com/James/LogicPrimer/Gates.html

En esta página del Profesor Efstathiou, los simuladores lógicos aparecen del lado derecho de la pantalla, en donde las opciones para simular las compuertas elementales que hemos visto son obtenidas del menú "Circuits" bajo las opciones "Gates 1" y "Gates 2" (hay otras opciones, las cuales serán tratadas en su debido momento en otros capítulos de este libro cuando el lector esté lo suficientemente familiarizado con el comportamiento de las tres funciones lógicas básicas).

Los enlaces proporcionados seguían siendo válidos al momento de ser publicada esta obra en Internet a principios de 2008. Desafortunadamente, no existe enlace alguno en Internet cuya vida esté garantizada a largo plazo. De cualquier modo, en caso de que desaparezcan algunos de los enlaces arriba citados, siempre hay la posibilidad de que los programas anteriormente recomendados se puedan encontrar en otros sitios o inclusive de que se pueda encontrar programas mejores que los ya señalados. Todo es cuestión de utilizar una buena maquinaria de búsqueda como Google.

Aunque no desempeña ninguna función lógica de ningún tipo, un componente que aparece con cierta frecuencia en el mundo de la lógica digital como indicador luminoso para proporcionar algún tipo de información visual al usuario es el diodo emisor de luz (light emitting diode ó LED):

el cual no sólo es un diodo en el sentido técnico dado a la palabra (un componente en el cual la corriente eléctrica puede fluír únicamente en un sentido pero no en el sentido contrario) sino que además es capaz de emitir luz de cierto color cuando se le aplica un voltaje con la polaridad correcta (con la polaridad del voltaje invertida, el LED no conducirá corriente alguna ni emitirá luz alguna). El diodo LED generalmente se construye con una terminal más corta (denominada cátodo ó terminal -) que la otra (denominada ánodo ó terminal +). A continuación tenemos un LED junto con el símbolo con el cual se le representa en los diagramas esquemáticos:

El diodo emisor de luz LED está disponible en varios colores, ya sea rojo, verde, azul, ó ambar como el que tenemos a continuación:

El esquema más sencillo para "encender" un diodo emisor de luz LED con una batería común y corriente E es el siguiente, en el cual basta con aplicarle el voltaje de la batería poniendo atención en la polaridad apropiada:

La resistencia R mostrada en el esquemático tiene como principal objetivo limitar la magnitud de la corriente eléctrica impidiendo que haya un corto circuito que dañaría al componente y al sistema, pero también tiene como objetivo fijar el valor de la corriente con la cual el LED podrá emitir su mayor brillo posible sin dañarse. Por no ser el diodo LED un diodo ideal sino un diodo real (el diodo ideal es aquél que al estar polarizado en un sentido actúa como un circuito abierto y al estar polarizado en el sentido inverso actúa como un circuito cerrado sin pérdidas de voltaje a través del mismo), cuando un diodo LED está conduciendo existe una pequeña caída de voltaje constante V_F (forward voltage) a través del mismo, la cual tiene que ser restada del voltaje de la batería E para determinar la magnitud de la corriente eléctrica que fluirá a través del mismo según la fórmula en el esquemático.

Una gran ventaja de los diodos emisores de luz LED es que por la relativamente pequeña cantidad de corriente eléctrica que requiren para "encenderse" se pueden conectar directamente a la salida de un circuito lógico ya sea para indicar una salida de "0" ó una salida de "1". Hay dos formas en las cuales se puede llevar a cabo la conexión, indicadas en los siguientes dibujos:

En el diagrama (1) de la izquierda, cuando la salida del NAND es "1" en realidad este componente estará poniendo un voltaje de algo así como unos +5 volts directamente a la entrada del diodo LED, y como el otro extremo del LED está conectado a través de la resistencia R al nivel de "0" ó "tierra eléctrica" (GND) estará polarizado justo en la forma correcta para "encender" indicando la presencia del "1" lógico a la salida del NAND. La resistencia R es utilizada para impedir un "corto-circuito" eléctrico y limitar la magnitud de la corriente justo a lo que requiere el diodo LED para poder encender adecuadamente. Y si la salida del NAND es "0" en realidad este componente no estará poniendo ningún voltaje a su salida que será de cero volts, con lo cual con ambos extremos del LED estará conectados a "tierra", con lo cual el LED estará apagado, indicando la presencia de un "0" lógico. En lo que respecta al diagrama (2) de la derecha, cuando la salida del NAND es "1" estará poniendo un voltaje de +5 volts en una terminal del LED, y como la otra terminal del LED también está conectada al mismo voltaje de +5 volts el LED no conducirá corriente eléctrica alguna permaneciendo apagado, ya que para poder "encender" el diodo LED tiene que tener su ánodo conectado a un "1" lógico y su cátodo conectado a un "0" lógico para que la corriente eléctrica pueda fluír en la dirección indicada por la flecha de su símbolo; no puede encender con ambas terminales conectadas a un "1" lógico. Por otro lado, cuando la salida del NAND es un "0" lógico, esto polariza al LED en la forma correcta y la corriente eléctrica puede fluír de "1" a "0" entrando por la terminal de salida del NAND. (No hay ninguna contradicción en que la terminal de salida del NAND actúe al mismo tiempo como una entrada de corriente eléctrica, ya que una cosa es el voltaje de cero volts puesto a la salida y otra cosa es la corriente eléctrica que le puede entrar a través de su terminal de salida; recuérdese siempre que los "ceros" y "unos" están definidos en función de la presencia o la ausencia de un voltaje.) La principal diferencia entre el circuito (1) de la izquierda y el circuito (2) de la derecha es que en el circuito de la izquierda el LED se enciende cuando la salida del NAND es "1" y se apaga cuando la salida del LED es "0", mientras que en el circuito de la derecha el LED se apaga cuando la salida del NAND es "1" y se enciende cuando la salida del NAND es "0".

Posiblemente una de las aplicaciones más útiles que pueda tener un diodo emisor de luz LED para el técnico especializado en dar mantenimiento a sistemas digitales sea en la construcción de la herramienta fundamental utilizada por dichos técnicos: la punta de prueba lógica (logic probe), como la siguiente:

Este tipo de puntas de prueba generalmente tienen dos diodos emisores de luz LED, uno para indicar una condición lógica de "0" (LOW ó LO) y el otro para indicar una condición lógica de "1" (HIGH ó HI). Generalmente no requieren de alguna fuente de energía interna (baterías), ya que toman su energía directamente del mismo circuito que está siendo analizado a través de unas terminales de tipo "caimán" (alligator clips). En la punta de prueba mostrada arriba, la terminal caimán de color rojo se conecta al polo positivo (+) de la fuente de poder, mientras que la terminal caimán de color negro se conecta al polo negativo (-) de la fuente. El interruptor selector en esta punta de prueba identificado como "TTL/CMOS" sirve para escoger los niveles adecuados de voltaje y corriente según sea la familia lógica a la cual pertenezca el componente que está siendo analizado, ya sea TTL ó CMOS (véase el Suplemento # 1: Las familias lógicas).

Aunque en manos de un técnico experto la punta de prueba lógica arriba mostrada sirve admirablemente para el análisis, diagnóstico y reparación de la gran mayoría de los sistemas digitales en uso comercial hoy en día, para ciertas aplicaciones sumamente especializadas en donde el presupuesto no es ningún problema existen otras puntas de prueba mucho más refinadas que en realidad son puntas de prueba lógicas sólo de nombre, ya que por su complejidad se trata en realidad de instrumentos de medición de alta precisión, como la "punta de prueba lógica" LogicDart de Hewlett-Packard:

Quizá lo más interesante de todo esto es que para la construcción de la "punta de prueba lógica" LogicDart utilizada para el mantenimiento de sistemas digitales basados ultimadamente en las tres funciones lógicas básicas se utilizaron circuitos integrados basados también ultimadamente en las tres funciones lógicas básicas.